במסגרת קורס למידת מכונה (מפוקחת) אצל ד״ר אבשלום אלמלח קיבלנו משימת אמצע לחזות ערכים רציפים באמצעות השוואה בין מספר מודלים רגרסיביים.
מטלה זו איפשרה לנו, לראשונה למעשה, להתנסות באופן מעשי בתהליך המחקרי שמאפיין את עבודתו של מדען נתונים – החל מניתוח נתונים ראשוני (EDA), דרך בניית מודלים ועד להשוואת ביצועים.
תרגיל חיזוי מחיר קופסת הרינג
דני, חובב הרינג, הבחין כי לקוחות שונים משלמים מחירים שונים על קופסת הרינג האהובה עליו. המוכר הסביר לו שהמחיר נקבע לפי סוג ההרינג ולפי התאמה אישית המבוססת על 10 פרמטרים.
דני ביקש מיוסי לאסוף נתונים – 1000 תצפיות עם 10 פרמטרים לכל תצפית ועמודת מחיר.
מטרת התרגיל:
בניית מודל לחיזוי מחיר קופסת הרינג בהתבסס על 10 פרמטרים.
שלבים בתרגיל:
- טעינת הנתונים.
- ניתוח והבנת הנתונים.
- הצגת 2–3 ויזואליזציות שמסייעות בהבנת הדאטה.
- אימון ארבעת המודלים הבאים תוך השוואת נתון ה-MAE שלהם: רגרסיה ליניארית, רגרסיה פולינומית, עץ החלטה, Random Forest.
- חיזוי על סט חדש - קובץ excel המכיל 1000 שורות.
- השתמשו במודל עם ה־Mean Absolute Error הנמוך ביותר כדי לחזות את עמודת המחיר.
- אין לבצע מחדש fit!
מבוא
במסגרת המטלה, נדרשנו לפתח מודל חיזוי למחיר קופסאות הרינג על סמך עשרה פרמטרים שנאספו בקפידה. התהליך כלל ניתוח מעמיק של הנתונים, אימון מודלים שונים והשוואת ביצועיהם, תוך דגש על מדד Mean Absolute Error (MAE) כמדד העיקרי להערכת איכות התחזיות.
הדוח מפרט את תהליך העבודה בכל אחד משלבי המשימה – החל מניתוח הנתונים הראשוני (EDA) דרך אימון מודלים שונים כמו רגרסיה ליניארית, רגרסיה פולינומית, עץ רגרסיה ויער אקראי ועד לבחירת המודל הטוב ביותר וחיזוי מחירי הקופסאות בקובץ הבדיקה.
מטרת הדוח היא לא רק להציג את התוצאות אלא גם לשתף בתהליך האנליטי שהוביל לפתרון. במהלך העבודה נעשה שימוש במגוון ויזואליזציות, שיטות סטטיסטיות וכלים ללמידת מכונה, על מנת להבטיח דיוק מרבי ואמינות גבוהה של המודל.
בדוח זה תמצאו תיאור מפורט של האופן בו טיפלנו בנתונים, ביצענו ניתוחים, קבענו היפרפרמטרים, והערכת ביצועי המודלים, לצד תובנות שהתקבלו במהלך התהליך.
מה זה למעשה Mean Absolute Error?
Mean Absolute Error (MAE) הוא מדד נפוץ להערכת ביצועי מודלים של חיזוי, המודד את הממוצע של הערכים המוחלטים של הסטיות בין הערכים החזויים לערכים האמיתיים. בניגוד ל-Mean Squared Error, ה-MAE אינו מעניש סטיות גדולות באופן לא פרופורציונלי, מה שהופך אותו למדד עמיד יותר בנוכחות ערכים חריגים. הנוסחה המתמטית של MAE מוגדרת כך:
$$MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|$$כאשר \( n \) הוא מספר הדגימות, \( y_i \) הוא הערך האמיתי, ו-\( \hat{y}_i \) הוא הערך החזוי.
ערך MAE נמוך יותר מעיד על התאמה טובה יותר של המודל לנתונים, כאשר MAE = 0 מציין התאמה מושלמת.
ומה לגבי R²?
מקדם הדטרמינציה (R²) הוא כלי סטטיסטי המודד את יכולת הניבוי של מודל. הוא מציג איזה אחוז מהשונות במשתנה התלוי ( \( y \)) מוסבר על-ידי המשתנים המסבירים (\( x \)).
ערכי R² נעים בין 0 ל-1, כאשר ערך גבוה (קרוב ל-1) מצביע על מודל שמסביר היטב את הנתונים, וערך נמוך (קרוב ל-0) מעיד על מודל חלש. חשוב לציין שאין להסתמך על R² בלבד בהערכת טיב המודל, במיוחד במודלים מורכבים, לא-ליניאריים או כאלה המכילים ריבוי משתנים.
הנוסחה לחישוב \( R^2 \) היא:
$$ R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2} $$כאשר:
- \( y_i \) הם הערכים האמיתיים,
- \( \hat{y}_i \) הם הערכים החזויים על ידי המודל,
- \( \bar{y} \) הוא הממוצע של כל הערכים התלויים.
ניתוח דאטה אקספלורטורי (EDA)
מבנה הנתונים
סט הנתונים לאימון מכיל 1000 שורות המתפרסים על פני 11 עמודות.
להלן מבנה העמודות וסיכום הערכים החסרים:
| שם עמודה | סוג העמודה | מספר ערכים חסרים |
|---|---|---|
| Feature1 | נומרית | 30 |
| Feature2 | נומרית | 30 |
| Feature3 | קטגוריאליות | 0 |
| Feature4 | קטגוריאליות | 0 |
| Feature5 | נומרית | 35 |
| Feature6 | נומרית | 31 |
| Feature7 | נומרית | 29 |
| Feature8 | נומרית | 27 |
| Feature9 | נומרית | 34 |
| Feature10 | נומרית | 35 |
| Price | נומרית | 0 |
סטטיסטיקות
באמצעות השימוש במתודה describe, הופקו הנתונים הסטטיסטיים עבור העמודות הנומריות.
בטבלה בחרתי להשמיט את העמודות Feature 3 ו-Feature4 מכיוון שהן מייצגות ערכים קטגוריאליים.
להלן הטבלה המייצגת את סיכום הנתונים:
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| Feature1 | 970.0 | 5.299010 | 31.986071 | 1.201504 | 3.592592 | 4.253486 | 4.918534 | 1000.000000 |
| Feature2 | 970.0 | 3.519229 | 32.269986 | -1000.000000 | 3.865050 | 4.563057 | 5.209897 | 7.738834 |
| Feature5 | 965.0 | 5.220990 | 32.071981 | 1.287018 | 3.477981 | 4.208140 | 4.855434 | 1000.000000 |
| Feature6 | 969.0 | 4.658473 | 1.014979 | 1.511661 | 3.939879 | 4.632781 | 5.361547 | 7.503020 |
| Feature7 | 971.0 | 2.764098 | 0.586462 | 2.000528 | 2.296842 | 2.638051 | 3.087333 | 5.243093 |
| Feature8 | 973.0 | 1.780509 | 32.154383 | -1000.000000 | 2.326696 | 2.677745 | 3.169590 | 5.852731 |
| Feature9 | 966.0 | 2.801546 | 0.611611 | 2.000207 | 2.324811 | 2.652079 | 3.179404 | 5.241267 |
| Feature10 | 965.0 | 2.812615 | 0.601790 | 2.000683 | 2.330789 | 2.691908 | 3.189667 | 5.926238 |
| Price | 1000.0 | 1059.096071 | 585.641730 | 164.392959 | 628.212162 | 942.850102 | 1347.441038 | 3905.449113 |
טיפול בנתונים חריגים
בחרתי לדגום את החריגים בשיעור של 20% - כך שיבדקו עשירון עליון ועשירון תחתון בלבד.
התפלגות החריגים לפני הסרה:
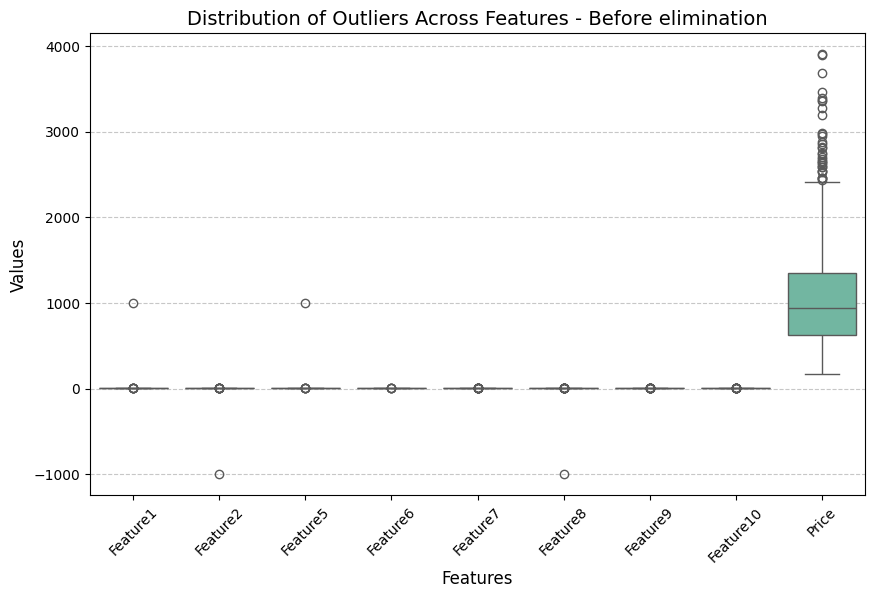
כמות השורות להסרה היא 7.
מספרי השורות שיש להסיר (אינדקסים):
[30, 237, 421, 631, 723, 848, 873].
התפלגות החריגים לאחר ההסרה:
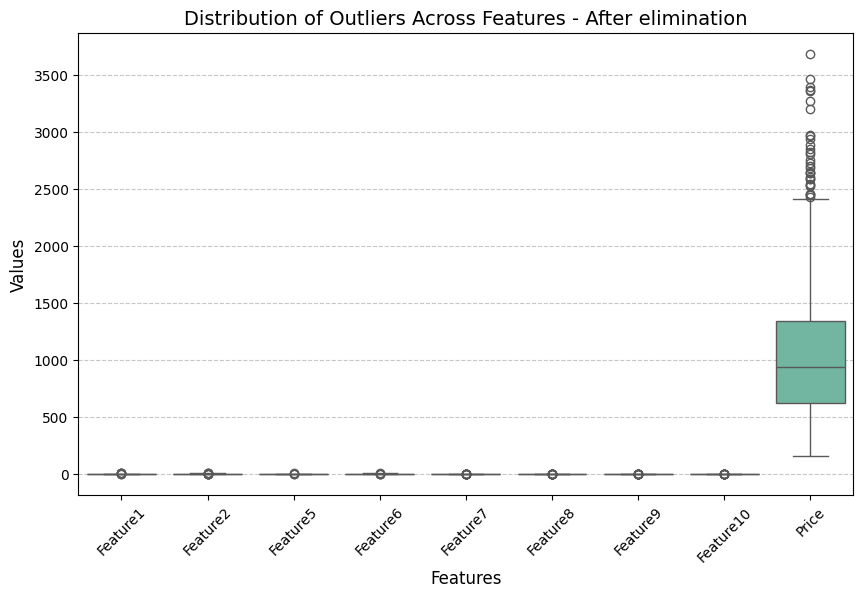
ניתן לראות בבירור את הסקאלה משתנה וגם את ההסרה של ארבעת החריגים בפיצ׳רים 1,2,5 וגם 8.
לאחר הסרת השורות המכילות ערכים קיצוניים נשארנו עם 993 שורות בסט נתוני האימון שלנו.
טיפול בערכים קטגוריאליים
טיפול בערכים קטגוריאליים הוא שלב חשוב בתהליך הכנת הנתונים עבור למידת מכונה, שכן רוב האלגוריתמים אינם מסוגלים להתמודד ישירות עם משתנים קטגוריאליים (כגון טקסט או קטגוריות). בסט הנתונים הזה זיהיתי שני פיצ’רים המוגדרים כערכים קטגוריאליים. על מנת שאוכל לבצע הליך למידת מכונה מדויק וחקירת נתונים יעילה, עלי להמיר את הערכים הקטגוריאליים לייצוג מספרי.
לכן, בחרתי להשתמש במתודה One-Hot Encoding.
מתודה זו ממירה כל קטגוריה לפיצ’ר חדש המיוצג על ידי ערכים בוליאניים (0 ו-1). היתרון המרכזי בשיטה זו הוא שמירה על מבנה הנתונים בצורה שאינה מטילה סדר או היררכיה על הקטגוריות.

הקוד של המתודה נראה כך:
# Encoding Feature 3 & Feature 4 columns.
columns_to_encode = ['Feature3', 'Feature4']
encoder = OneHotEncoder(sparse_output=False, drop='if_binary', handle_unknown='ignore')
encoded_features = encoder.fit_transform(dataset[columns_to_encode])
encoded_df = pd.DataFrame(encoded_features, columns=encoder.get_feature_names_out(columns_to_encode))
dataset = dataset.drop(columns=columns_to_encode)
dataset = pd.concat([dataset, encoded_df], axis=1)
column_to_move = 'Price'
# Move the column to the last position
dataset = dataset[[col for col in dataset.columns if col != column_to_move] + [column_to_move]]
dataset.head(2)
טיפול בנתונים חסרים
$$ Values_m = \frac{264}{1000} $$
השלמת הנתונים החסרים:
מכיוון שאין לנו מידע מלא על כלל העמודות הנומריות הבלתי תלויות, בחרתי להשתמש ב-IterativeImputer להשלמת הערכים החסרים, במקום להשלים באמצעות ממוצע.
הבחירה ב-IterativeImputer נועדה למנוע יצירת הטיה סטטיסטית כלפי ערכי הממוצע, במיוחד כאשר מדובר בכמות משמעותית של נתונים חסרים.
imputer = IterativeImputer(max_iter=10, random_state=42)
dataset = pd.DataFrame(imputer.fit_transform(dataset), columns=dataset.columns)
יתרונות השיטה:
- מתחשב בקשרים בין כל העמודות ומשתמש במודלים רגרסיביים להשלמת הערכים.
- מאפשר ניצול מלא של המבנה המורכב של הנתונים.
מטריצת קורלצייה
בכדי להציג את המטריצה בצורה הטובה ביותר ולהניב ממנה תובנות אמיתיות בחרתי לבודד את העמודות הקטגוריאליות שלנו לטובת בחינת הקשר בין העמודות הנומריות בלבד.
פעולה זו מפחיתה את ההשפעה של נתונים שאינם מספריים, שעלולים להטות את הניתוח ולפגוע בדיוק התובנות.
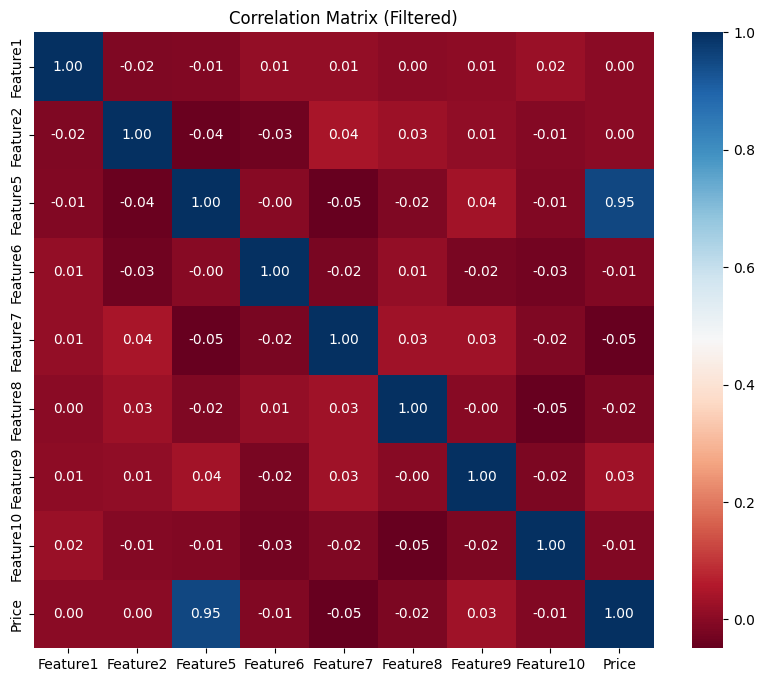
שתי תובנות מרכזיות שעלו לאחר התבוננות במטריצת הקורלציה המצורפת:
- רוב ערכי הקורלציה במטריצה נעים סביב 0 מה שמעיד על כך שאין קשר ליניארי חזק בין רוב המשתנים.
- בין פיצ’ר 5 לבין המשתנה התלוי שלנו קיימת קורלציה חזקה שעשויה לרמז ש-Feature5 עשוי להיות מנבא חזק של המחיר או תלוי בו באופן הדוק.
Variance Inflation Factor
ביצעתי בדיקה למדידת מידת המולטיקולינאריות (ליניאריות בין פיצ’רים) בנתונים – ואלה תוצאותיה:
| feature | VIF |
|---|---|
| const | 177.306074 |
| Feature1 | 1.001323 |
| Feature2 | 1.005786 |
| Feature5 | 1.006014 |
| Feature6 | 1.003496 |
| Feature7 | 1.006715 |
| Feature8 | 1.004253 |
| Feature9 | 1.003322 |
| Feature10 | 1.004733 |
מתוצאות בדיקה זו ניתן להסיק את הדברים הבאים:
פיצ’רים (Feature1 עד Feature10):
- כל ערכי ה-VIF של הפיצ’רים הם סביב 1.00 זהו סימן מצוין לכך שאין כמעט מולטיקולינאריות בין הפיצ’רים.
- הפיצ’רים נראים עצמאיים מבחינה ליניארית, ולכן אין צורך להסיר אף אחד מהם או לבצע אלימינציה כל שהיא.
הקבוע (const):
ערך ה-VIF עבור ה-const (קבוע במודל) גבוה מאוד: 177.31.
זהו מצב נורמלי במקרים שבהם קיימת עמודת קבוע (intercept) במודל, כיוון שהקבוע תמיד תלוי לחלוטין בנתונים (כל הערכים זהים). ערך זה אינו מצביע על בעיה וניתן להתעלם ממנו.
מסקנות:
ערכי VIF של הפיצ’רים עצמם מצביעים על נתונים נקיים ממולטיקולינאריות.
ולכן לא נדרשת אלימינציה מכל סוג.
ריגרסיה ליניארית
אקדים ואומר שיחס התלות בין המשתנים לא מצביע על אפשרות להשתמש במודל של רגרסיה ליניארית. אך מכיוון שנתבקשו לעשות כך אדגים את השימוש ברגרסיה זו על גבי המטלה.
במסגרת המטלה אימנתי מודל ריגרסיה ליניארית. מנתוני המודל אוכל להגיד בפה מלא כי הנתונים הללו פשוט אינם מתאימים לרגרסיה ליניארית.
| 120.865 | Mean Absolute Error |
|---|---|
| 0.896 | R² |
120.87 מצביע על הטעות הממוצעת האבסולוטית בתחזיות המודל.
R² Score של 0.896 (כ-90%) מעיד על כך שהמודל מסביר 90% מהשונות בנתונים. זהו ערך גבוה, המעיד על התאמה טובה -לכאורה- בין המודל לנתונים, אך עלי לבדוק אם הנ"ל משקף מודל כללי או שיש חשש לאוברפיטינג.
לסיכום
המודל מצליח להסביר את רוב השונות (R² גבוה), אך ישנן בעיות חמורות בנתונים בגלל הפיצ’רים הקטגוריאליים שגורמים להטיה חמורה של המודל. להוסיף שערכי המקדמים (Coefficients) של המודל מצביעים על חוסר איזון.
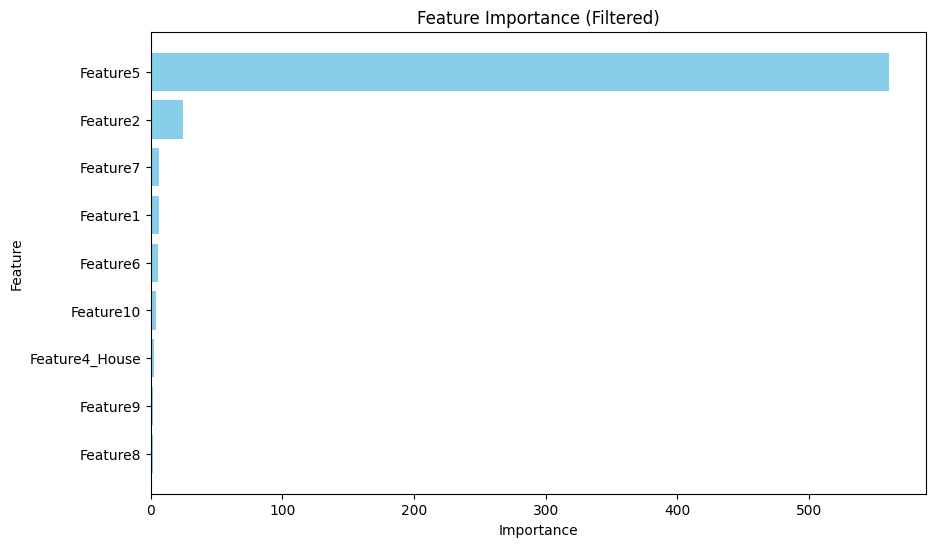
חשיבות פיצ’רים (Feature Importance)
הרצתי בדיקה אחר המשתנים החשובים ביותר ואלו תוצאותיה:
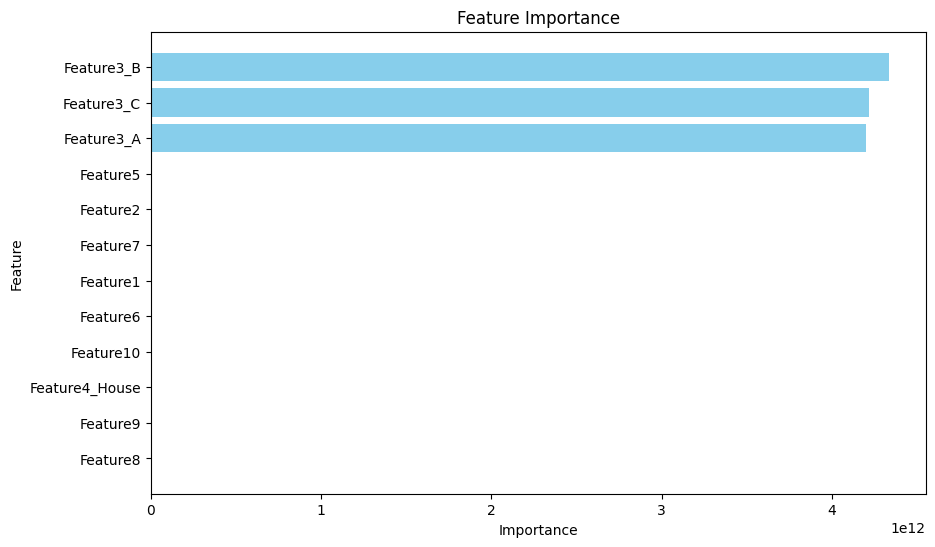
מכיוון שהפיצ׳רים המשמעותיים ביותר יצאו קטגוריים החלטתי שאני רוצה לבודד אותם בכדי לראות את השתנה הרציף המשפיע ביותר:
גרף Residuals VS Predicted
הגרף Residuals vs Predicted הוא כלי חשוב באבחון מודלים של רגרסיה, ותפקידו המרכזי הוא לבדוק את אחת ההנחות החשובות במודלים אלו: שהשגיאות (Residuals) מפוזרות בצורה אקראית.
$$ \text{Residual} = y - \hat{y} $$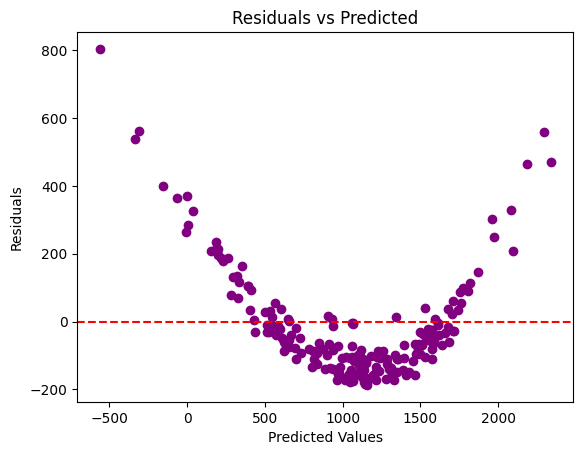
מהגרף ניתן ללמוד שהשאריות מציגות תבנית בצורה פרבולה או “U” מובהקת:
זהו סימן לכך שהמודל לא מתאים היטב לנתונים, כלומר הוא אינו מתאר את המבנה האמיתי של הקשר
בין המשתנים בצורה מיטבית. מה שמחדד את הנחת היסוד שלי שהקשר בין המשתנים אינו ליניארי.
ניתן לראות שבאזורים מסוימים (למשל בערכים נמוכים וגבוהים) השאריות מתרחקות משמעותית מ-0. דבר שעשוי להעיד על הטרוסקדסטיות (heteroscedasticity), כלומר שונות לא אחידה בנתונים.
ומכאן הגיעו לאימון מודלים נוספים
אני לא רוצה לחפור פה מידי. מי שירצה יוכל להריץ את הקוד המלא ב-Github שלי.
אני אגיד שאחרי שהרצתי מודל ליניארי (ששוב אני מדגיש, לא מתאים לסט הנתונים הזה) הרצתי גם מודל פולינומי, עץ החלטה וגם Random Forest (שבעברית נקרא - יער אקראי? מוזר).
בסופו של דבר המודל שהצליח לתת את הדיוק הרב ביותר היה ה-Random Forest וכפי שתוכלו לראות בטבלה הבאה הפער בינו לבין שאר המודלים היה לא קטן:
| MAE | R² | |
|---|---|---|
| ריגרסיה ליניארית | 120.865 | 0.896 |
| ריגרסיה פולינומית | 34.483 | 0.993 |
| עץ החלטה | 41.10 | 0.989 |
| RANDOM FOREST | 32.903 | 0.993 |
בכדי להגיע לתוצאות הללו יצרתי לולאה שבודקת בטווח של עד 60 עצים ובקפיצות של 10, ובעומק של עד 10 שכבות מה היא הקומבינציה האופטימלית ביותר וקיבלתי את הפלט הבא:
| Value | Feature |
|---|---|
| 40 | n_estimators |
| 9 | max_depth |
| 32.9 | MAE |
| 0.9936 | R² |
לאחר מכן, טענתי לתוכנה את קובץ ה-TEST ועליו ביצעתי חיזוי למחיר בהתבסס הלמידה שביצעתי עם היער האקראי. מוזמנים לצפות בפרוייקט ב-GIT שלי, בקישור הזה.
כמה מילות סיכום 🤍
למעשה מדובר בפרוייקט הראשון שאימנתי מספר מודלים וחקרתי בכוחות עצמי.
רגע שהיה מרגש מאוד - היא אותה נקודת מעבר מהחומרים התיאורטיים ליישום הפרקטי שלהם תוך כדי זה שהרגשתי איך הלכה למעשה חושי המחקר שלי מתחדדים ואני לאט לאט מתחיל ׳ללעוס׳ את הדאטה ומצליח לייצר מודלים שהם מדוייקים יותר ויותר.
יש משהו קסום בלהסתכל על נתונים ולדעת לחבר את המודל הטוב ביותר עבורם.
ויש אפילו משהו מספק מאוד בלדעת שצדקת לכל אורך הדרך והצלחת להביא את החוזי המדוייק ביותר.
מכאן כמובן שיעלו פה פרוייקטים מעניינים ואיכותיים יותר.
