מבוא
למידה מפוקחת (Supervised learning) היא סוג של למידת מכונה שבה הערכים שצריך לחזות כבר ידועים, והמטרה היא לבנות מודל שמסוגל לחזות בצורה מדויקת ערכים של נתונים שטרם נראו.
למידה מפוקחת עושה שימוש במאפיינים (features) על מנת לחזות את הערך של משתנה המטרה (target variable), כמו למשל חיזוי מיקומו של שחקן כדורסל על פי ממוצע הנקודות שלו למשחק.
סוגי למידה מפוקחת
ישנם שני סוגים של למידה מפוקחת:
- סיווג (Classification)- משמש לחיזוי התווית או הקטגוריה של תצפית. לדוגמה, ניתן לחזות האם עסקה בנקאית היא הונאה או לא. מכיוון שיש כאן שני תוצאות אפשריות – עסקה הונאתית או עסקה שאינה הונאתית – זה נקרא סיווג בינארי.
- רגרסיה (Regression)- משמשת לחיזוי ערכים רציפים. לדוגמה, מודל יכול להשתמש במאפיינים כמו מספר חדרי השינה וגודל הנכס כדי לחזות את משתנה המטרה – מחיר הנכס.
שפה
שימו לב כי מה שאנחנו מכנים מאפיין (feature), אחרים עשויים לכנות משתנה מנבא (predictor variable) או משתנה בלתי תלוי (independent variable). בנוסף, מה שאנחנו מכנים משתנה מטרה (target variable), אחרים עשויים לכנות משתנה תלוי (dependent variable) או משתנה תגובה (response variable).
דברים שחשוב לזכור לפני שמבצעים למידה מפוקחת
לפני שמתחילים לעבוד עם למידה מפוקחת, צריך לוודא כמה דברים לגבי הנתונים:
- אסור שיהיו לנו ערכים חסרים.
- כלל נתוני הלמידה חייבים להיות בפורמט מספרי
- צריכים להיות שמורים כ-DataFrames או Series של pandas, או כמערכים (arrays) של NumPy.
כדי לוודא שהכל מסודר כמו שצריך, כדאי להתחיל מניתוח נתונים ראשוני.
אפשר להשתמש בכלים של pandas לניתוחים בסיסיים ולשלב גם גרפים שיעזרו להבין את הנתונים טוב יותר.
עקרונות בסיסיים של Scikit-Learn
scikit-learn משתמשת באותה תחביר עבור כל המודלים של למידה מפוקחת, מה שהופך את תהליך העבודה לאחיד ולחוזר על עצמו. לפני שנעבוד עם נתונים אמיתיים, נכיר את התחביר הכללי של העבודה עם scikit-learn.
from sklearn.module import Model
model = Model()
model.fit(X,y)
prediction = model.predict(X_new)
print(prediction)
בתחילה, מייבאים מודל (Model) – שהוא סוג של אלגוריתם שמתאים לבעיה שלנו – מתוך מאגר המודלים של sklearn. לדוגמה, המודל Logistic regression שהיא מודל לחיזוי הסתברות של משתנה תלוי בינארי (כמו 0 או 1), באמצעות שילוב לינארי של מאפיינים והמרת התוצאה לפונקציה לוגיסטית שתוחמת את הערכים בטווח שבין 0 ל-1.
לאחר מכן, יוצרים משתנה בשם model ומאתחלים אותו כמודל שבחרנו. בשלב הבא, “מתאימים” (fit) את המודל לנתונים שלנו, כלומר, נותנים לו ללמוד את הקשרים בין המאפיינים (features) לבין משתנה המטרה (target variable). ההתאמה מתבצעת באמצעות העברת X, מערך המאפיינים שלנו, ו-y, מערך הערכים של משתנה המטרה.
בסיום, נשתמש במתודת predict של המודל כדי לחזות ערכים חדשים בהתבסס על הלמידה שביצע המודל.
קלסיפיקציות / סיווג
כעת נדון כיצד לבנות מודל סיווג (classifier) שיכול לחזות את התוויות של נתונים שלא נראו בעבר.
ישנם ארבעה שלבים עיקריים:
ראשית, אנו בונים מסווג (classifier), שלומד מתוך הנתונים המתויגים שאנו מעבירים אליו.
לאחר מכן, אנו מעבירים לו נתונים לא מתויגים כקלט, והוא חוזה תוויות עבור הנתונים החדשים.
הנתונים המתויגים שמהם המסווג לומד נקראים נתוני אימון (training data).
עכשיו הגיע הזמן לעשות תאכלס
בואו נבנה את המודל הראשון שלנו! נשתמש באלגוריתם בשם k-Nearest Neighbors, או KNN, שהוא פופולרי לפתרון בעיות סיווג.
הרעיון של KNN הוא לחזות את התווית של כל נקודת נתון על ידי הסתכלות על k, למשל שלוש, נקודות הנתונים המתויגות הקרובות ביותר, ולתת להן “להצביע” איזו תווית הנתון החדש צריך לקבל.
KNN מבצע חיזוי לפי הצבעת רוב – הוא בוחר את התווית שמופיעה אצל רוב השכנים הקרובים.
דוגמה עם גרף פיזור:
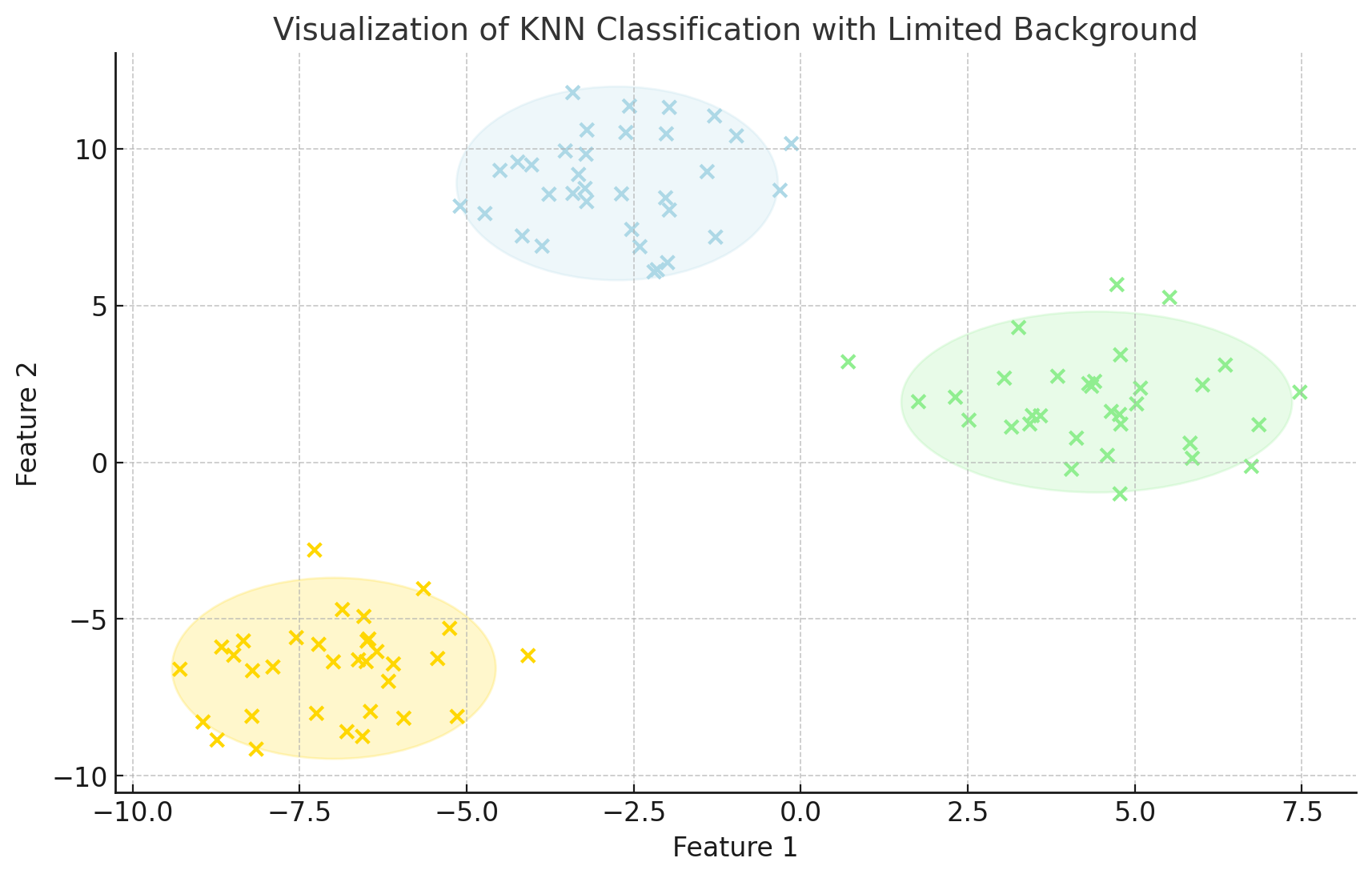
הסבר - נניח ויש לנו איזה שהיא נקודה במרחב ואנחנו קובעים ש-k יהיה 5.
אז מה שיקרה ברקע זה שהמודל יסתכל על חמשת הנקודות הקרובות ביותר לנקודה שלנו ויסווג אותה על פי עקרון הרוב.
קטע קוד טיפוסי לשימוש עם מסווג מסוג k-Nearest Neighbors:
# יבוא הספריה
from sklearn.neighbors import KNeighborsClassifier
# הגדרת הצירים שלנו
y = churn_df["churn"].values
X = churn_df[["account_length", "customer_service_calls"]].values
# יצירת המסווג לפי הסתכלות על חמשת השכנים הקרובים ביותר
knn = KNeighborsClassifier(n_neighbors=5)
# אימון המודל
knn.fit(X,y)
# חוזי
y_pred = knn.predict(X_new)
# הדפסת החוזי
print("Predictions: {}".format(y_pred))
דוגמאות נפוצות לשימוש בקלסיפיקציה
הלכה למעשה אנחנו עושים שימוש בכלי סיווג בכל פעם שאנחנו רוצים ללמד מכונה למיין עבורנו נתונים או לחזות את המיון העתידי שלהם:
- הונאות אשראי- מיון בזמן אמת מנעד רחב של עסקאות אשראי לטובת עצירת עסקאות להן מאפיינים הונאתיים.
- נטישת לקוחות - מודל של קלסיפיקציה בינארית יאפשר לנו לתכלל מערך נתונים שידע לנבא האם לקוח מסויים עתיד לעזוב את שירותי החברה שלי?
- סיווג מיילים כדואר זבל (SPAM) - שירותי דואר רבים מיישמים מודלים כאלה בכדי לנתב הודעות נכנסות לתיבת דואר זבל.
- זיהוי מחלות רפואיות - סיווג האם מטופל סובל ממחלה מסויימת בהתבסס על נתונים קליניים או תמונות רפואיות.
- זיהוי תמונות או אובייקטים
- אבטחת סייבר- סיווג בקשות רשת כבטוחות או זדוניות בהתאמה.
- ניבוי הצלחה בלימודים - סיווג סטודנטים ‘בסיכון נשירה’ או ‘מצליחים’ לפי נתוני נוכחות, ציונים ועוד
מדידת ביצועי המודל - דיוק
$$ Accuracy = \frac{Correct \ \ predictions}{Total \ \ Observations} $$לא ניתן לחשב את הדיוק על בסיס הנתונים ששימשו לאימון הסיווג מכיוון שנתונים אלו שימשו לאימון המודל, ולכן אחוז הדיוק לא ישקף את יכולתו של המודל להכליל נתונים שלא נראו בעבר. דוגמא לקוד המאפשר לנו לבדוק את מידת דיוק המודל שלנו:
# Import the module
from sklearn.model_selection import train_test_split
X = churn_df.drop("churn", axis=1).values
y = churn_df["churn"].values
# Split into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=None)
knn = KNeighborsClassifier(n_neighbors=5)
# Fit the classifier to the training data
knn.fit(X_train, y_train)
# Print the accuracy
print(knn.score(X_test, y_test))
# Output
0.8545
פיצול סט הנתונים לאימון ולבדיקה
flowchart LR
A[Spliting The Data]
subgraph Splitted Dataset
direction TB
B[Training Set]
C[Test set]
end
A --> B
A --> C
B --> D[Fit / Train on training set]
C --> E[Calculate Accuracy using TEST SET ONLY]
D --> E
classDef lightblue fill:#E3F2FD,stroke:#90CAF9,stroke-width:1px;
class Z,A,B,C,D,E lightblue;
נהוג לפצל את סט הנתונים שלנו כך ש-20%-30% ממנו ישמש את המודל לבדיקה.
נתונים הנבחרים לשמש את המודל לבדיקת רמת הדיוק- בהכרח לא יופעלו בשלב האימון.
sklearn מאפשרת לנו לחלק את הנתונים בצורה אוטומטית על ידי שימוש במתודה שנקראת train_test_split- את השימוש במתודה אנחנו נבצע באמצעות דוגמאת הקוד הבאה:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, stratify=y)
הפרמטר random_state מאפשר לקבוע זרע (seed) למחולל המספרים האקראיים המשמש בתהליך חלוקת הנתונים, מה שמבטיח שהחלוקה תהיה ניתנת לשחזור בכל הפעלה מחדש.
חשוב במיוחד כאשר נרצה לוודא שהניסוי או המודל שלנו מייצרים את אותן תוצאות בתנאים זהים.
בכדי לשמור על עקביות ביחס בין הקטגוריות (labels) בנתונים, נשתמש בפרמטר stratify, אשר מבטיח שיחס הקטגוריות בקבוצות האימון והבדיקה ישקף את היחס שלהן בנתונים המקוריים. לדוגמה, אם 10% מהנתונים מייצגים עזיבת לקוח, השימוש ב-stratify יבטיח שאותו יחס יישמר הן בקבוצת האימון והן בקבוצת הבדיקה, מה שמונע הטיות שעלולות לפגוע ביכולת המודל להכליל את התוצאות.
מורכבות המודל
אחד האתגרים המרכזיים שאנחנו מתמודדים איתם בעת בניית המודל הוא האיזון בין פשטות המודל לבין מורכבותו, בכדי למטב את ביצועי המודל.
שני מושגים מרכזיים בהקשר זה הם תת-התאמה (Underfitting) ו-התאמת יתר (Overfitting).
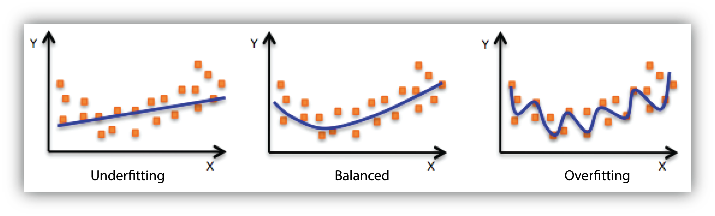
מהי תת-התאמה (Underfitting)?
תת-התאמה מתרחשת כאשר המודל פשוט מדי ואינו מצליח ללמוד את הקשרים והדפוסים המשמעותיים בנתונים. במצב זה, המודל אינו מספק ביצועים טובים לא על קבוצת האימון ולא על קבוצת הבדיקה. דוגמאות למצבים של תת-התאמה:
- מודלים עם מעט מדי פרמטרים.
- שימוש בפונקציות ליניאריות לנתונים בעלי קשרים מורכבים יותר.
תוצאה: המודל מספק תחזיות גרועות, מכיוון שהוא מפספס מידע חשוב מתוך הנתונים.
מהי התאמת יתר (Overfitting)?
התאמת יתר מתרחשת כאשר המודל מורכב מדי, ומתאים את עצמו באופן מדויק מדי לנתוני האימון, כולל רעשים ודפוסים אקראיים שאינם מייצגים את המידע הכללי. במצב זה, המודל עשוי להציג דיוק גבוה על קבוצת האימון, אך ייכשל בביצועים על נתונים חדשים מקבוצת הבדיקה. דוגמאות למצבים של התאמת יתר:
- מודלים עם מספר רב של פרמטרים ביחס לכמות הנתונים.
- שימוש במודלים שמגיבים חזק לרעש בנתוני האימון.
תוצאה: המודל אינו מצליח להכליל מגמות כלליות בנתונים, ולכן התחזיות שלו עבור נתונים חדשים אינן מדויקות.
הדגמה באמצעות מודל KNN
במודלים כמו KNN (k-Nearest Neighbors), ניתן לאזן בין תת-התאמה להתאמת יתר על ידי בחירה בערך מתאים של הפרמטר n_neighbors, המייצג את מספר השכנים שהמודל משתמש בהם לקבלת החלטה.
- ערך נמוך של
n_neighborsעלול להוביל להתאמת יתר, שכן כל תצפית בודדת משפיעה משמעותית על גבול ההחלטה. - ערך גבוה של
n_neighborsעלול להוביל לתת-התאמה, מכיוון שהמודל מתעלם מפרטים חשובים ומתאים החלטותיו רק למגמות כלליות.1
רגרסיה
$$ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_n X_n + \epsilon $$מתי עושים שימוש ברגרסיה?
רגרסיה משמשת במצבים שונים, ביניהם:
- ניתוח קשרים בין משתנים- הבנת ההשפעה של משתנה אחד על משתנה אחר (למשל, איך גיל והשכלה משפיעים על שכר).
- תחזיות - חיזוי ערכים רציפים, כמו הערכת מחיר בית על סמך מאפיינים כמו שטח, מיקום ומספר חדרים.
- זיהוי דפוסים - חשיפת מגמות ותבניות בתוך הנתונים.
סוגי רגרסיות
- לינארית - מודל פשוט שבו הקשר בין המשתנים מיוצג באמצעות קו ישר (לדוגמה, חיזוי משקל על פי גובה).
- לוגיסטית - משמשת לניבוי ערך קטגורי (לדוגמה, האם אדם יעבור מבחן – כן או לא); למרות שזו אינה רגרסיה במובן המסורתי.
- פולינומית - משמשת לתיאור קשרים לא לינאריים, שבהם הקשר בין המשתנים מתבטא בעקומה ולא בקו ישר.
- רב-משתנית (Multiple Regression) - גרסה של רגרסיה לינארית המשלבת מספר משתנים בלתי תלויים להשפעה על משתנה תלוי אחד.
- לא לינארית - מיועדת למצבים שבהם הקשרים בין המשתנים מורכבים ולא ניתנים לתיאור באמצעות מודל לינארי.
הערכת ביצועים
פונקציית הפסד (LOSS FUNCTION)
$$ MSE = \frac{1}{n} \sum_{i=1}^n (\hat{y}_i - y_i)^2 $$ציון R²
מדד R² נקרא גם מקדם ההסבר, הוא מדד סטטיסטי המשמש להערכת איכות ההתאמה של מודל רגרסיה לנתונים.
משמעות:
- מייצג את אחוז השונות במשתנה המטרה שמוסבר על ידי המשתנים המסבירים במודל.
- הערך של המדד נע בין:
0: המודל אינו מסביר כלל את השונות.
1: המודל מסביר באופן מלא את השונות במשתנה המטרה.
כאשר הנוסחא מחושבת לפי 1 פחות סכום ריבועי השגיאות לחלק בסך השונות.
Cross Validation
כאשר מחשבים את ערך ה-R² על קבוצת הבדיקה שלנו, חשוב להבין שהתוצאה תלויה באופן שבו חילקנו את הנתונים!
ייתכן מאוד שלנתונים בקבוצת הבדיקה יש מאפיינים מסוימים שאינם מייצגים את יכולת המודל להיכליל על נתונים שלא נראו קודם. ולכן בכדי להתמודד עם התלות הזו, הנובעת מחלוקה אקראית, משתמשים בטכניקה הנקראת קרוס-ולידציה (Cross-Validation).
מהי קרוס-ולידציה?
נתחיל בחלוקה של מערך הנתונים שלנו לחמישה חלקים (או “קפלים”, Folds). בכל שלב נשאיר קפל אחד כקבוצת בדיקה, ונאמן את המודל על ארבעת הקפלים הנותרים.
לאחר מכן נבצע חיזוי על קבוצת הבדיקה ונחשב את המדד שאותו אנו בודקים, לדוגמה R-squared.
את התהליך חוזרים על כל קפל:
- בשלב הראשון הקפל הראשון הוא קבוצת הבדיקה.
- בשלב השני הקפל השני הוא קבוצת הבדיקה, וכן הלאה.
- כך אנו מקבלים חמישה ערכים של R-squared (או כל מדד אחר שנבחר) מהם ניתן לחשב ממוצע, חציון ועוד.
כמה קפלים לבחור?
כאשר אנו מחלקים את הנתונים לחמישה קפלים, התהליך נקרא 5-fold Cross-Validation. אם נבחר בעשרה קפלים, הוא ייקרא 10-fold Cross-Validation. באופן כללי, התהליך נקרא k-Fold Cross-Validation, כאשר k מייצג את מספר הקפלים. עם זאת, יש פה טרייד-אוף: ככל שמספר הקפלים גדול יותר, כך התהליך דורש יותר משאבים חישוביים, משום שהמודל מאומן ומבצע חיזויים מספר רב יותר של פעמים.
יישום ב-Python עם scikit-learn
כדי לבצע קרוס-ולידציה ב-scikit-learn, נייבא את הפונקציות הדרושות cross_val_score מתוך sklearn.model_selection ואת KFold.
נגדיר את המודל (למשל, רגרסיה לינארית) ונעביר אותו יחד עם הנתונים לפונקציה cross_val_score, תוך שימוש באובייקט ה-KFold שהגדרנו. הפונקציה תחזיר מערך של תוצאות עבור כל אחד מהקפלים.
from sklearn.model_selection import cross_val_score, KFold
kf = KFold(n_splits=5, shuffle=True, random_state=1)
regressor = LinearRegression()
cv_result = cross_val_score(regressor, X, y, cv=kf)
ניתוח התוצאות
התוצאות כוללות את ערכי המדד (למשל, R-squared) עבור כל קפל. נוכל לחשב:
- ממוצע באמצעות np.mean.
- סטיית תקן עם np.std.
- רווחי סמך של 95% בעזרת np.quantile.
print(cv_results)
print(np.mean(cv_results), np.std(cv_results)
print(np.quantile(cv_results, [0.25, 0.975]))
באמצעות קרוס-ולידציה, אנו מקבלים הערכה מדויקת יותר של יכולת המודל להכליל על נתונים חדשים, ומוודאים שהתוצאות אינן תלויות בחלוקה ספציפית אחת של הנתונים.
בשביל הנוחות צרפתי פה שרטוט2 אשר מסביר מבחינה ויזואלית על הצד הטוב ביותר איך עובד תהליך ה-Cross Validation:

סיכום הפוסט: למידה מפוקחת - הצעד הראשון שלך בלמידת מכונה
בפוסט זה הצגנו את יסודות הלמידה המפוקחת (Supervised Learning) – תחום מרכזי בלמידת מכונה שבו בונים מודלים לחיזוי ערכים על סמך נתונים מתויגים. דנו בשני הסוגים המרכזיים: סיווג (Classification) לחיזוי תוויות, ו-רגרסיה (Regression) לחיזוי ערכים רציפים.
עברנו על מושגים חשובים, כמו מאפיינים (Features) ומשתנה מטרה (Target Variable), והצגנו כלים להיערכות נכונה עם הנתונים – החל מניקוי הנתונים ועד לחלוקה לסטים לאימון ולבדיקה.
הדגמנו את תחביר העבודה עם ספריית Scikit-Learn, המאפשרת לנו להגדיר מודלים, לאמן אותם ולחזות תוצאות בצורה פשוטה ויעילה. בין הדוגמאות שהוצגו: מודל KNN לסיווג, רגרסיה ליניארית, והחשיבות של מדידת ביצועים כמו דיוק וציון R².
לבסוף, עסקנו בטכניקת Cross-Validation שמאפשרת להעריך בצורה מדויקת את יכולת ההכללה של המודל. למדנו על האיזון בין פשטות למורכבות מודל, ועל הסיכונים שבתת-התאמה (Underfitting) והתאמת יתר (Overfitting).
הפוסט הזה הוא רק ההתחלה – שילוב של תיאוריה ופרקטיקה, צעד ראשון לעולם הרחב והמלהיב של למידת מכונה. בפוסטים הבאים נעמיק ונצלול לעומק באתגרים ובשיטות מתקדמות.
המסע אל המודל המנצח מתחיל מכאן. 🚀
-
התמונה נלקחה מהמאמר של AWS בנושא Model Fit: Underfitting vs. Overfitting ↩︎
-
נוצר על ידי: Gufosowa - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=82298768 ↩︎
